문제
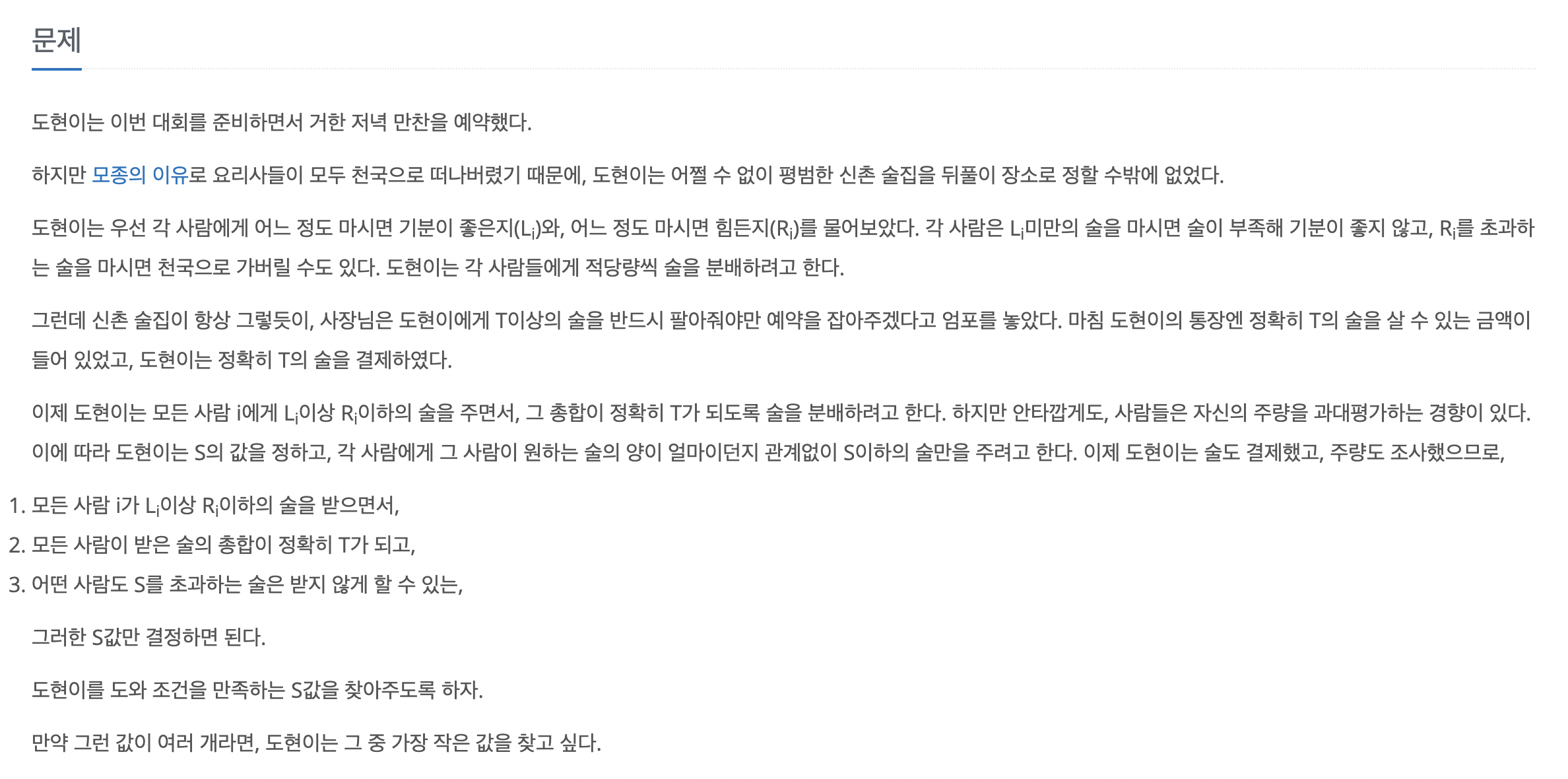
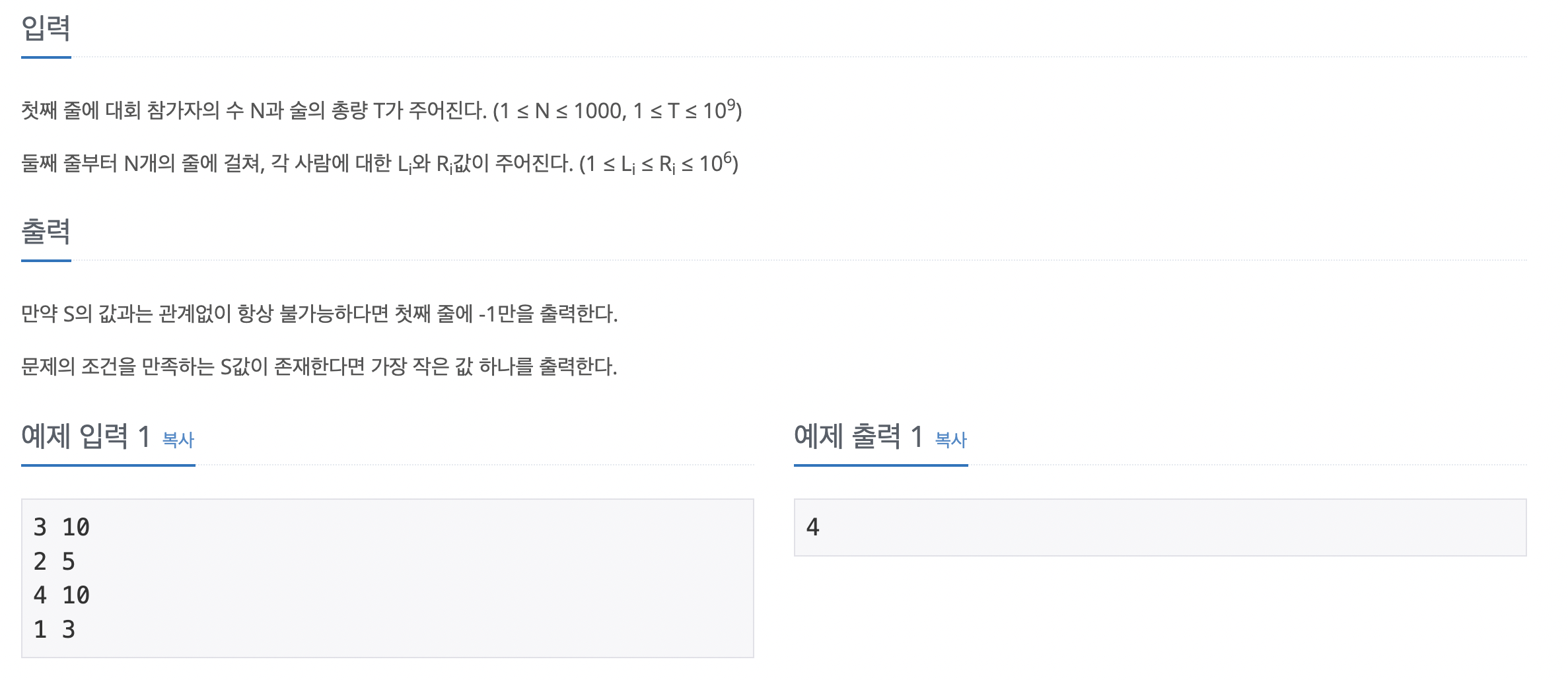
풀이
파라매트릭 서치(매개변수 탐색) 문제입니다.
이분탐색으로 값의 범위를 좁혀나가면서 현재 값이 문제의 조건을 만족하냐 만족하지 않느냐를 판단해주면 됩니다.
1. 입력받기
N = Integer.parseInt(st.nextToken());
T = Integer.parseInt(st.nextToken());
arr = new int[N][2];
for(int i=0; i<N; ++i) {
st = new StringTokenizer(br.readLine());
arr[i][0] = Integer.parseInt(st.nextToken());
arr[i][1] = Integer.parseInt(st.nextToken());
}arr은 (N x 2) 2차원 배열로 다음의 값이 저장됩니다.
arr[i][0]: Li. 즉 i번째 사람이 기분 좋아지려면 마셔야하는 최소 술의 양
arr[i][1]: Ri. 즉 i번째 사람이 천국에 가지 않는 최대 술 양
2. 파라매트릭 서치
우선 큰 틀은 아래와 같이 이분탐색 로직입니다.
while문 안에는 mid(=구해야하는 S값)가 조건에 맞는지를 판단하고, 올바른 S 값을 찾기 위해서 left, right 값을 조정해주는 부분입니다.
int left = 0;
int right = 1_000_001;
int ans = Integer.MAX_VALUE;
while(left <= right) {
int mid = (left + right) / 2;
// .. mid 값(= 구해야하는 S 값)이 조건에 맞는지 판단하고 조정하는 부분
}3. can 메서드
mid 값이 조건에 부합하는지 판단하는 메서드(can() 메서드)를 따로 만들어서 판단해줍니다.
private static int can(int num) {
int lower = 0, upper = 0;
for(int i=0; i<N; ++i) {
if(arr[i][0] > num) return 1; // (1) num을 늘려야함
lower += arr[i][0]; // (2)
upper += Math.min(num, arr[i][1]); // (3)
}
if(lower <= T && upper >= T) return 0; // (4) 가능
else if (lower > T) return -1; // (5) num을 줄여야 함
else return 1; // (6) num을 늘려야 함
}여기서 num을 S라고 생각해주시면 더 이해가 쉽습니다.
이 can 메서드는 S값을 늘려야하면 1을, 줄여야하면 -1을, S가 조건을 충족하면 0을 리턴합니다.
주석을 봐주시면
(1): Li가 S(num)보다 큰 경우이므로, 이 경우에는 i번째 사람이 취할 수가 없어서 S 값을 늘려야합니다.
(2): lower에는 필요한 최소 술의 양이 저장됩니다. (L의 합)
(3): upper에는 필요한 최대 술의 양의 저장됩니다. 이때, S가 Ri보다 크면 i번째 사람이 천국에 가므로, S와 Ri 중 작은 값을 더해줍니다.
(4): 만약 T 값이 lower, upper 사이의 값이면 해당 num 값은 S 값으로서 적절합니다. T가 lower, upper 사이에 위치하기만 하면 그 안에서는 모든 술의 합이 T가 되도록 조정이 가능하기 때문입니다.
(5): 만약 T가 lower 밑이라면? S를 줄여서 lower 값을 더 줄여야 합니다.
(6): 만약 T가 upper보다 크다면 S값을 늘려서 upper 값을 더 늘려야 합니다.
4. mid가 S로서 적절한지 판단
int left = 0;
int right = 1_000_001;
int ans = Integer.MAX_VALUE;
while(left <= right) {
int mid = (left + right) / 2;
if(can(mid) == 0) {
right = mid - 1;
ans = Math.min(ans, mid);
} else if(can(mid) > 0) {
left = mid + 1;
} else {
right = mid - 1;
}
}
if (ans == Integer.MAX_VALUE) {
ans = -1;
}
System.out.println(ans);can(mid)값이
0일 때: S의 값으로 적절하므로 ans의 값을 ans와 mid 중 최소값으로 바꾸어주고, 더 작은 S값이 있을 수 있으니 right = mid -1로 바꿔서 다시 탐색해줍니다.
1일 때: mid값이 더 커져야하므로, left = mid+1로 바꿔서 다시 탐색해줍니다.
-1일때: mid값이 더 작아져야하므로, right = mid-1로 바꿔서 다시 탐색해줍니다.
만약 while문을 빠져나왔을 때, ans의 값이 Integer.MAX_VALUE 이면, 조건을 만족하는 S값이 존재하지 않는다는 것이므로 -1로 바꿔서 출력합니다.
전체 코드
import java.io.*;
import java.util.*;
class Main {
static int N, T;
static int[][] arr;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
T = Integer.parseInt(st.nextToken());
arr = new int[N][2];
for(int i=0; i<N; ++i) {
st = new StringTokenizer(br.readLine());
arr[i][0] = Integer.parseInt(st.nextToken());
arr[i][1] = Integer.parseInt(st.nextToken());
}
int left = 0;
int right = 1_000_001;
int ans = Integer.MAX_VALUE;
while(left <= right) {
int mid = (left + right) / 2;
if(can(mid) == 0) {
right = mid - 1;
ans = Math.min(ans, mid);
} else if(can(mid) > 0) {
left = mid + 1;
} else {
right = mid - 1;
}
}
if (ans == Integer.MAX_VALUE) {
ans = -1;
}
System.out.println(ans);
}
private static int can(int num) {
int lower = 0, upper = 0;
for(int i=0; i<N; ++i) {
if(arr[i][0] > num) return 1; // num을 늘려야함
lower += arr[i][0]; //
upper += Math.min(num, arr[i][1]);
}
if(lower <= T && upper >= T) return 0; // 가능
else if (lower > T) return -1; // num을 줄여야 함
else return 1; // num을 늘려야 함
}
}'Algorithm > 백준' 카테고리의 다른 글
| [Java / 백준] 4781. 사탕 가게 (3) | 2024.07.03 |
|---|---|
| [백준 / Java] 2141. 우체국 (5) | 2024.06.25 |
| [백준 / Java] 2665. 미로만들기 (2) | 2024.06.11 |
| [ 백준 / Java ] 2573. 빙산 (0) | 2024.06.04 |
| [백준 / Java] 2477. 참외밭 (2) | 2024.05.28 |



